Materi Fisika Listrik: Juli 2018

Sabtu, 21 Juli 2018

Soal Dan Jawaban Materi Fisika Listrik

Muatan Listrik
Dua muatan listrik Q1 dan Q2 menimbulkan gaya tolak – menolak sebesar F pada saat jarak antara kedua muatan r. Jika gaya tolak – menolak menjadi 4F, maka jarak antara kedua muatan menjadi …

JAWAB

F1 = F
r1 = r
F2 = 4F
r2 = …?
Besarnya jarak pada keadaan kedua adalah..

$\frac { { F }_{ 1 } }{ { F }_{ 2 } } ={ \left( \frac { { r }_{ 2 } }{ { r }_{ 1 } } \right) }^{ 2 }\\ \\ \frac { F }{ 4F } ={ \left( \frac { { r }_{ 2 } }{ { r } } \right) }^{ 2 }\\ \\ \sqrt { \frac { F }{ 4F } } =\quad \frac { { r }_{ 2 } }{ { r } } \\ \\ \sqrt { \frac { 1 }{ 4 } } =\frac { { r }_{ 2 } }{ { r } } \\ \\ \frac { 1 }{ 2 } =\frac { { r }_{ 2 } }{ { r } } \\ \\ { r }_{ 2 }\quad =\quad \frac { 1 }{ 2 } r$

Daya Listrik

Sebuah mesin sepeda motor melakukan usaha sebesar 10.000 joule. Jika daya motor itu 2000 watt, hitunglah waktu yang digunakan ?

Pembahasan

W = 10.000 J
P = 2000 Watt
W = P . t
t =

t =

10.0002000

= 5 detik
Jadi waktu yang diperlukan motor itu adalah 5 detik.

Medan Listrik

Titik A berada pada jarak 5 cm dari muatan +10 mikro Coulomb. Besar dan arah medan listrik pada titik A adalah… (k = 9 x 10⁹Nm²C⁻², 1 mikro Coulomb = 10⁻⁶ C)
Pembahasan
Diketahui :

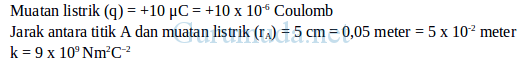
Ditanya : Besar dan arah medan listrik pada titik A
Jawab :

Arah medan listrik di titik A :
Muatan listrik positif karenanya arah medan listrik menjauhi muatan listrik dan menjauhi titik A.

Potensial Listrik

Tentukan potensial listrik pada suatu titik berjarak 1 cm dari muatan q = 5,0 μC. Konstanta Coulomb (k) = 9 x 10⁹ Nm²C⁻², 1 μC = 10⁻⁶ C.
Pembahasan
Diketahui :
Jarak dari muatan (r) = 1 cm = 1/100 m = 0,01 m = 10^-2 m
Muatan (q) = 5,0 μC = 5,0 x 10^-6 Coulomb
Ditanya : Potensial listrik (V)
Jawab :
Potensial listrik :

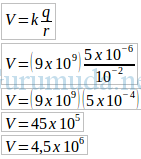Potensial listrik adalah 4,5 x 10⁶ Volt.

Listrik Dinamis

Jika dalam kawat mengalir kuat arus sebesar 5 A. Berapakah jumlah muatan yang melewati luas penampang kawat dalam waktu 1 menit ?

Pembahasan

I =

5 =

q60

q = 5 x 60 = 300 Coulomb

Hukum Kirchoff 1

Sebuah rangkaian memiliki 6 buah arus (I1, I2, I3, I4, I5, dan I6) seperti gambar di bawah. Besarnya arus masing-masing adalah 6, 5, 3, 4, dan 2 dalam satuan Ampere (A). Berapakah besarnya arus I6?

Diketahui:

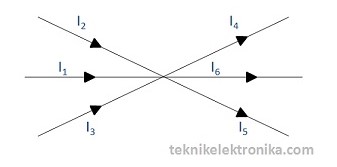
Sumber: teknikelektronika.com

I1 = 6A, I2 = 5A, I3 = 3A, I4 = 4A, dan I5 = 2A

Ditanya:

I6?

Jawab:

pakai teori hukum Kirchoff 1:

∑Imasuk = ∑Ikeluar

I1 + I2 + I3 = I4 + I5 + I6

6 + 5 + 3 = 4 + 2 + I6

14 = 6 + I6

8 A = I6

Jadi, besarnya I6 adalah 8 A.

Hukum Kirchoff 2

Perhatikan aliran besar kuat arus pada sebuah rangkaian listrik berikut ini!

Pembahasan:

Diketahui:

R1 = 2 Ω
R2 = 3 Ω
R3 = 3 Ω
V1 = 12 V
V2 = 12 V

Berapakah besar arus listrik pada rangkaian tersebut?

Untuk memecahkan soal ini, Anda terlebih dahulu harus menentukan arah arus dan arah loopnya.

Menerapkan Hukum Kirchoff 2!

ε + I R + 0 atau ΣE +ΣIR = 0

– 12 V + i . 2Ω – 12 V + i . 3Ω + 3 Ω = 0

– 24 V + i . 8 Ω = 0

i . 8Ω = 24 V

i = 24 V / 8 Ω = 3 A

Rangkaian Resistor

Rangkaian Seri

Hitunglah hambatan total pada gambar rangkaian seri di bawah ini! Jika R1 = 5 Ω, R2 = 10 Ω, dan R3 = 3 Ω.

Rangkaian Paralel

Berikut ini latihan soal rangkaian paralel. Carilah hambatan totalnya! R1 = 6 Ω, R2 = 12 Ω,
contoh soal rangkaian paralel

Rangkaian Campuran/Gabungan

Berikut ini gambar rangkaian campuran atau kombinasi rangkaian seri dan paralel. Tentukan nilai hambatan totalnya! R1 = 4 Ω, R2 = 6 Ω, dan R3 = 3 Ω.

contoh soal rangkaian campuran dan pembahasannya

Rangkaian Kapasitor

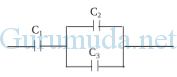
Tiga kapasitor terangkai seri-paralel seperti pada gambar di bawah. Jika C1 = 2 μF, C2 = 4 μF, C3 = 4 μF, maka kapasitas penggantinya adalah…

Contoh soal kapasitor – rangkaian seri dan paralel 1

Pembahasan:

Diketahui :

Kapasitor C1 = 2 μF
Kapasitor C2 = 4 μF
Kapasitor C3 = 4 μF
Ditanya : Kapasitas pengganti (C)
Jawab :
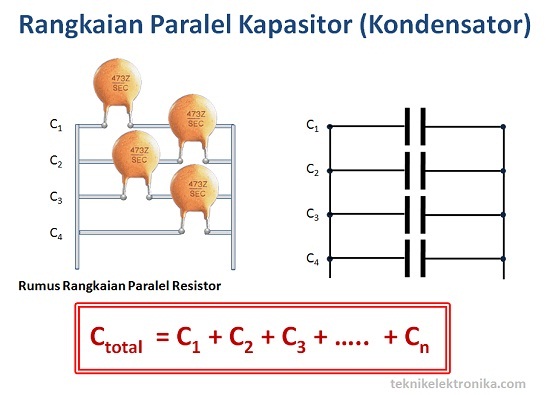
Kapasitor C2 dan C3 terangkai paralel. Kapasitas penggantinya adalah :
CP = C2 + C3 = 4 + 4 = 8 μF

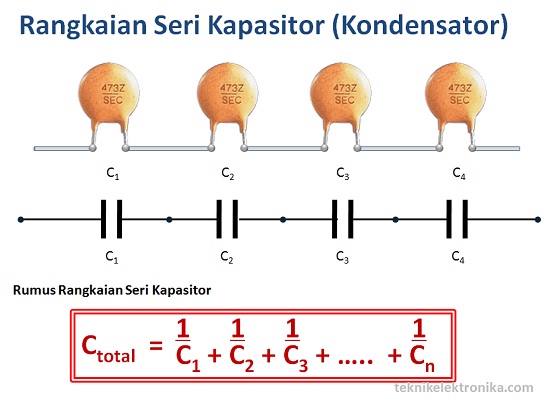
Kapasitor C1 dan CP terangkai seri. Kapasitas penggantinya adalah :
1/C = 1/C1 + 1/CP = 1/2 + 1/8 = 4/8 + 1/8 = 5/8
C = 8/5 μF

μF = mikro Farad (satuan kapasitansi listrik). 1 μF = 10^-6 Farad.

Minggu, 15 Juli 2018

Rangkaian Kapasitor

Kapasitor (Kondensator)

adalah Komponen Elektronika yang berfungsi untuk menyimpan Muatan Listrik dalam waktu yang relatif dengan satuannya adalah Farad. Variasi Nilai Farad yang sangat besar mulai dari beberapa piko Farad (pF) sampai dengan ribuan Micro Farad (μF) sehingga produsen komponen Kapasitor tidak mungkin dapat menyediakan semua variasi nilai Kapasitor yang diinginkan oleh perancang Rangkaian Elektronika.

Rangkaian Paralel Kapasitor

Rangkaian Paralel Kapasitor adalah Rangkaian yang terdiri dari 2 buah atau lebih Kapasitor yang disusun secara berderet atau berbentuk Paralel. Dengan menggunakan Rangkaian Paralel Kapasitor ini, kita dapat menemukan nilai Kapasitansi pengganti yang diinginkan.

Rumus :

C_total= C₁ + C₂ + C₃ + C₄ + …. + C_n

Dimana :

C_total= Total Nilai Kapasitansi Kapasitor
C₁     = Kapasitor ke-1
C₂    = Kapasitor ke-2
C₃    = Kapasitor ke-3
C₄    = Kapasitor ke-4
C_n     = Kapasitor ke-n

Contoh kasus untuk menghitung Rangkaian Paralel Kapasitor

Seorang Perancang Rangkaian Elektronika ingin merancang sebuah Peralatan Elektronika, salah satu nilai Kapasitansi yang diperlukannya adalah 2500pF, tetapi nilai tersebut tidak dapat ditemukannya di Pasaran Komponen Elektronika. Oleh karena itu, Perancang Elektronika tersebut menggunakan Rangkaian Paralel untuk mendapatkan nilai kapasitansi yang diinginkannya.

Penyelesaian :

Beberapa kombinasi yang dapat dipergunakannya antara lain :

1 buah Kapasitor dengan nilai 1000pF
1 buah Kapasitor dengan nilai 1500pF

C_total= C₁ + C₂
C_total= 1000pF + 1500pF
C_total= 2500pF

Atau

1 buah Kapasitor dengan nilai 1000pF
2 buah Kapasitor dengan nilai 750pF

C_total= C₁ + C₂ + C₃
C_total= 1000pF + 750pF + 750pF
C_total= 2500pF

Rangkaian Seri Kapasitor

Rangkaian Seri Kapasitor adalah Rangkaian yang terdiri dari 2 buah dan lebih Kapasitor yang disusun sejajar atau berbentuk Seri. Seperti halnya dengan Rangkaian Paralel, Rangkaian Seri Kapasitor ini juga dapat digunakan untuk mendapat nilai Kapasitansi Kapasitor pengganti yang diinginkan. Hanya saja, perhitungan Rangkaian Seri untuk Kapasitor ini lebih rumit dan sulit dibandingkan dengan Rangkaian Paralel Kapasitor.

Rumus dari Rangkaian Seri Kapasitor adalah :

1/C_total= 1/C₁ + 1/C₂ + 1/C₃ + 1/C₄ + …. + 1/C_n

Dimana :

C_total= Total Nilai Kapasitansi Kapasitor
C₁     = Kapasitor ke-1
C₂    = Kapasitor ke-2
C₃    = Kapasitor ke-3
C₄    = Kapasitor ke-4
C_n     = Kapasitor ke-n

Contoh kasus untuk menghitung Rangkaian Seri Kapasitor

Seorang Engineer ingin membuat Jig Tester dengan salah satu nilai Kapasitansi Kapasitor yang paling cocok untuk rangkaiannya adalah 500pF, tetapi nilai 500pF tidak terdapat di Pasaran. Maka Engineer tersebut menggunakan 2 buah Kapasitor yang bernilai 1000pF yang kemudian dirangkainya menjadi sebuah Rangkaian Seri Kapasitor untuk mendapatkan nilai yang diinginkannya.

Penyelesaian :

2 buah Kapasitor dengan nilai 1000pF

1/C_total= 1/C₁ + 1/C₂
1/C_total= 1/1000 + 1/1000
1/C_total= 2/1000
2 x C_total = 1 x 1000
C_total = 1000/2
C_total = 500pF

Rangkaian Campuran

Jaringan campuran kapasitor merupakan jaringan gabungan antara rangkaian seri dan paralel atau sebaliknya.

Nilai kapasitas penggantinya (Ct) terdiri dari (Cs) kapasitas seri dan (Cp) kapasitas paralel harus dihitung dengan cara menghitung salah satu rangkaian terlebih dahulu. Jika kapasitor dirangkai seri-paralel maka nilai Cs harus dihitung terlebih dahulu kemudian menghitung Ct. Jika kapasitor dirangkai paralel-seri maka harus menghitung nilai Cp kemudian menghitung nilai Ct.

Contoh soal :

3 buah kapasitor dihubung seri paralel dengan nilai C1 = C3 = 100μF , dan 50μF. Berapa Farad nilai kapasitas penggantinya?

Diketahui :

C1 = 100 μF

C2 = 50 μF

C3 = 100 μF

Ditanya : Ct = ?

Jawab : Kapasitor yang dirangkai seri dihitung terlebih dahulu (C1 dan C2) :

Menghitung Ct :